pure tones & complex sounds
Although frequency variations are probably the sound characteristic that we can hear more clearly, we left it as last, to conclude the discussion about the physical qualities of sound.
We have briefly defined what frequency is: the number of cycles that a waveform completes in a unit of time. We also said that frequency is measured in Hertz (Hz) and Kilohertz (KHz). 1Hz is equal to 1 cycle in 1 second.
On the other hand, we did not introduce the concept of shape of a sound wave: so far we have only examined sine waves, which are a very particular kind of waves. A sine represents the simplest sound we can hear: a single frequency that remains constant in time. This is also called a pure tone; we have listened to a 1KHz pure tone already, so let's hear a few more:
As you can hear, changing the frequency of a sound is equal to changing its pitch. however, because of their simplicity, pure sounds are very different from the notes generated by musical instruments. This is because those 'notes' are more complex sounds. Complex means that a sound is not just a single frequency as a pure tone, but it is made of more sounds at the same time.
Let's compare a guitar note and a pure tone of the same pitch:
When a guitar string is plucked, for example, it vibrates at a frequency which is called the primary resonant, whose value will depend on different factors such as the string diameter, its tension etc. This frequency is called the fundamental frequency, and it is the one that determines what we call the pitch of a note. In this case the fundamental is 440Hz (the A string). However if we compare it to a pure tone, we can tell that there is much more going on in a guitar note: we can clearly hear a 440Hz tone in the guitar note, but we also hear the following:
Play the guitar note once, and then a pure tone: can you hear all these pure tones in the guitar note?
You should be able to distinguish the 440Hz very clearly, and the rest of the tones should be progressively softer as their frequency increases. When we pluck a string, other than vibrating at its fundamental frequency (440Hz), its halves will vibrate at a frequency double of the fundamental (880Hz). Its thirds will vibrate at a frequency triple of the fundamental (1320Hz) and so on, theoretically to infinity. These frequencies are called 'partial frequencies', and are also known as 'harmonics'.
Let's take a look:
So being our fundamental frequency 440Hz:
The amplitude of the harmonics decreases progressively, so that at some stage it will become so soft that it could not be heard anymore.
Harmonics are theoretically exact multiples of the fundamental, but physical characteristics of musical instruments add a certain degree of approximation to these values.
In addition to harmonics, other sounds are produced when playing an instrument, that are not mathematically related to the fundamental note, the overtones: these sounds mostly depend on how the instrument is played, so imagine for example the difference between a guitar string plucked with fingertips, nails, or a plectrum. Overtones depend on countless variables, and together with the harmonics contribute to create the spectrum of a sound. The spectrum of a sound, is one of the main variables that are part of a sound timbre.
So, pure sounds are pretty rare to find in music, however it is important that we know how to distinguish them because they are the basis of more complex sounds. In other word, everything we hear, however complex, it is nothing but a sum of pure tones of different frequencies, amplitude and phase relationships.
This theory was first formulated by Jean Baptiste Joseph Fourier in the early 19th century. Fourier was a French physicist and a great mathematician. Thanks to his 'transformation' (so is called the mathematical algorithm at the basis of his theory), it is possible to identify the pure tones that form a complex sound. In our field we used the Fast Fourier Transform (FFT) which is extremely useful when we approach equalisation and frequency processing of a sound. By knowing what are the components of a complex sound (e.g. a musical instrument) we can change its sound properties.
We will not go into the details of Fourier's equations, but we will take a look at some examples:
Instead of visualising a waveform in the domain of time (x) and amplitude (y), thanks to the FFT we can see it in the domains of frequency (x) and amplitude (y) in a given moment of time. In the examples below, you can see the waveform on top, and a simplified FFT of that waveform just below, as white dots.
A sine, as we said, only contains one pure tone
This waveform is the sum of the previous sine and one of the same amplitude but double frequency (fundamental + second harmonic)
Here is what happens if we add a third harmonic. Its amplitude will be half of the fundamental's
There are some waveforms of specific shapes that have specific harmonic content, in the next lesson we will examine them thoroughly.
We have briefly defined what frequency is: the number of cycles that a waveform completes in a unit of time. We also said that frequency is measured in Hertz (Hz) and Kilohertz (KHz). 1Hz is equal to 1 cycle in 1 second.
On the other hand, we did not introduce the concept of shape of a sound wave: so far we have only examined sine waves, which are a very particular kind of waves. A sine represents the simplest sound we can hear: a single frequency that remains constant in time. This is also called a pure tone; we have listened to a 1KHz pure tone already, so let's hear a few more:
As you can hear, changing the frequency of a sound is equal to changing its pitch. however, because of their simplicity, pure sounds are very different from the notes generated by musical instruments. This is because those 'notes' are more complex sounds. Complex means that a sound is not just a single frequency as a pure tone, but it is made of more sounds at the same time.
Let's compare a guitar note and a pure tone of the same pitch:
When a guitar string is plucked, for example, it vibrates at a frequency which is called the primary resonant, whose value will depend on different factors such as the string diameter, its tension etc. This frequency is called the fundamental frequency, and it is the one that determines what we call the pitch of a note. In this case the fundamental is 440Hz (the A string). However if we compare it to a pure tone, we can tell that there is much more going on in a guitar note: we can clearly hear a 440Hz tone in the guitar note, but we also hear the following:
Play the guitar note once, and then a pure tone: can you hear all these pure tones in the guitar note?
You should be able to distinguish the 440Hz very clearly, and the rest of the tones should be progressively softer as their frequency increases. When we pluck a string, other than vibrating at its fundamental frequency (440Hz), its halves will vibrate at a frequency double of the fundamental (880Hz). Its thirds will vibrate at a frequency triple of the fundamental (1320Hz) and so on, theoretically to infinity. These frequencies are called 'partial frequencies', and are also known as 'harmonics'.
Let's take a look:
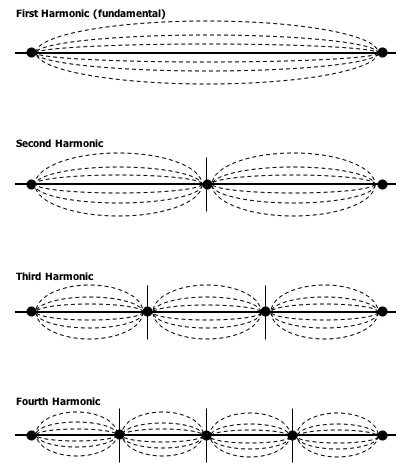
So being our fundamental frequency 440Hz:
| Note > | Frequency (Hz) | Fundam. times |
| Fundamental (first harmonic) | 440 | 1 |
| Second harmonic | 880 | 2 |
| Third harmonic | 1320 | 3 |
| Fourth harmonic | 1760 | 4 |
| Fifth harmonic | 2.200 | 5 |
| Sixth harmonic | 2.640 | 6 |
| Seventh harmonic | 3.080 | 7 |
Harmonics are theoretically exact multiples of the fundamental, but physical characteristics of musical instruments add a certain degree of approximation to these values.
In addition to harmonics, other sounds are produced when playing an instrument, that are not mathematically related to the fundamental note, the overtones: these sounds mostly depend on how the instrument is played, so imagine for example the difference between a guitar string plucked with fingertips, nails, or a plectrum. Overtones depend on countless variables, and together with the harmonics contribute to create the spectrum of a sound. The spectrum of a sound, is one of the main variables that are part of a sound timbre.
So, pure sounds are pretty rare to find in music, however it is important that we know how to distinguish them because they are the basis of more complex sounds. In other word, everything we hear, however complex, it is nothing but a sum of pure tones of different frequencies, amplitude and phase relationships.
This theory was first formulated by Jean Baptiste Joseph Fourier in the early 19th century. Fourier was a French physicist and a great mathematician. Thanks to his 'transformation' (so is called the mathematical algorithm at the basis of his theory), it is possible to identify the pure tones that form a complex sound. In our field we used the Fast Fourier Transform (FFT) which is extremely useful when we approach equalisation and frequency processing of a sound. By knowing what are the components of a complex sound (e.g. a musical instrument) we can change its sound properties.
We will not go into the details of Fourier's equations, but we will take a look at some examples:
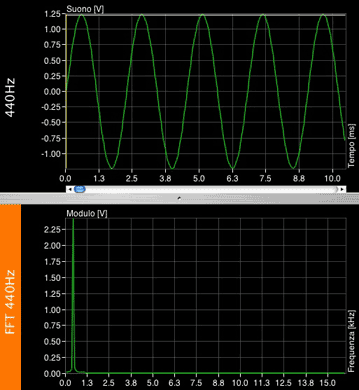
Instead of visualising a waveform in the domain of time (x) and amplitude (y), thanks to the FFT we can see it in the domains of frequency (x) and amplitude (y) in a given moment of time. In the examples below, you can see the waveform on top, and a simplified FFT of that waveform just below, as white dots.
A sine, as we said, only contains one pure tone
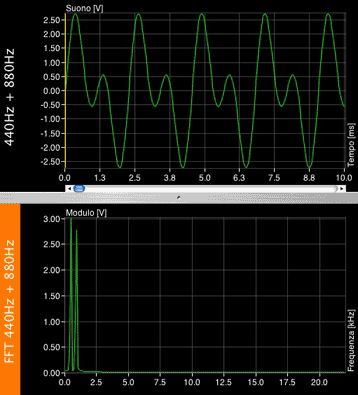
This waveform is the sum of the previous sine and one of the same amplitude but double frequency (fundamental + second harmonic)
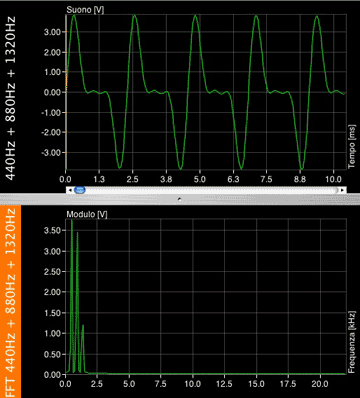
Here is what happens if we add a third harmonic. Its amplitude will be half of the fundamental's
There are some waveforms of specific shapes that have specific harmonic content, in the next lesson we will examine them thoroughly.
